Graph Writing # 102 - Stages and equipment used in the cement-making process
- Details
- Last Updated: Thursday, 04 August 2022 12:32
- Written by IELTS Mentor
- Hits: 345219
IELTS Academic Writing Task 1/ Graph Writing - Diagram/ Process Diagram:
» You should spend about 20 minutes on this task.
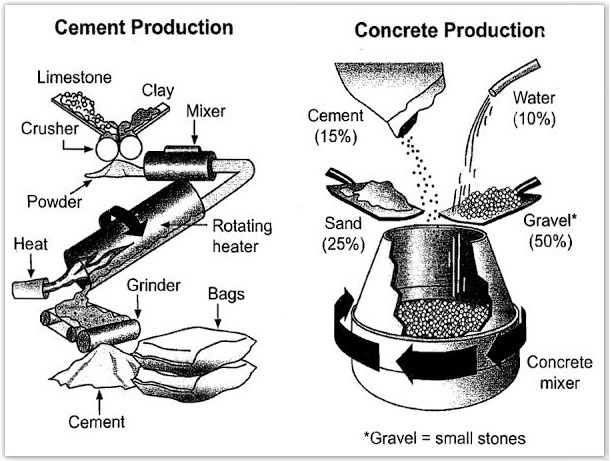
The diagrams below show the stages and equipment used in the cement-making process, and how cement is used to produce concrete for building purposes.
Summarise the information by selecting and reporting the main features, and make comparisons where relevant.
» Write at least 150 words.
Sample Answer 1:
The diagrams show the process of cement production and then how this cement is used for concrete production. As is observed from the graph, cement production involves some complex processes and concrete production is done using the water, cement and sand in a concrete mixer.
The first diagram depicts that, to produce cement first the limestone and clay are crushed and the produced powder from this is passed through a mixer. The power is then passed via a rotating heater where heat is supplied constantly and this process creates the raw cement materials which are passed on a grinder machine to finally produce the cement. The cement is then packed and marketed for sale.
The second diagram presents how the concrete is produced for housing and building work. In the first stage, 15% cement, 10% water, 25% sand and 50% small stones are mixed in a concrete mixer machine and the machine rotates fast to have the ingredients mixed together to create the concrete.
Sample Answer 2:
The two diagrams illustrate the cement-making process. We can see from the given illustration that cement is manufactured first, and then it's used in the concrete production.
In the first diagram, we can see that limestone is the raw material with which clay added. Firstly, the two materials are crushed to form the powder. Then this powder passes through a mixer and a heater through which the powder is exposed to flame. The powder now is in the form of a paste. This paste is grinded to be cement to pass through the last process; packing in bags.
The second diagram shows that cement can be used to produce concrete. This process is simpler than cement production; concrete is a mixture of 15% cement, 10 % water, 25% sand and 50 % small stones which are named as "Gravel". The four elements are poured in a huge mixer which rotates producing concrete. We can see that once the cement is produced by several steps and equipment, it can be used in other less complicated processes, for instance, concrete production.
(Submitted by Abdullah Hassan)
Sample Answer 3:
These two diagrams reveal the flow diagrams of both cement and concrete production processes with necessary equipment and materials that are used. Mainly, both processes have similarities and differences. They are similar because each of them has more than one input and a single output. On the other hand, they differ in the number of production steps.
In the cement production diagram, firstly, limestone and clay are gathered and passed through a crusher. Then, the powder obtained from crusher is moved to the mixer to make a homogene mixture. Next, rotating heater welcomes the material from the mixer. After heating step, resulting material flows on the grinder. Finally, cement becomes ready to be packed in bags at the end of the grinder.
In the concrete production diagram, the process contains only one step to have concrete material that is mixing. Cement, water, sand and gravel which is a general name for small stones are all mixed in a rotating concrete mixer in precise proportions such as 15%, 10%, 25% and 50% respectively.
(Submitted by Hüsna Uçar)
Sample Answer 4:
The diagrams illustrate how cement is produced and also an example of cement utilisation produced to make concrete to use in a form of construction.
To begin with, cement is produced by combining raw materials like limestone, clay, which are processed in a tool called crusher. Those all items are mixed together to create a perfect blend. The blend, furthermore, goes into to a rotating heater. As it is in the rotating heater tube, heat is introduced from the end of the tube before the blend is actually dropped onto grinder. Then, after all the systemic process, the mixture turns into some cement which is then packed into bags.
Meanwhile, to create concrete, the main components of construction systems are gravel, cement, water, sand and a concrete mixer to blend all the materials. Gravel or small stone is the major and biggest component needed and accounts for 50% among all materials. There are, however, some other materials like the sand which is mainly used and comes in the second place and is accounted halved from gravel, followed by cement and water. The cement accounts for 15% compared to among all materials used to construct a new real construction. All the material is mixed together by a concrete mixer.
Overall, the steps of making cement are more complicated and require advanced machinery while concrete production requires mixing required components in the right proportion in a simpler machine. While heat is required to produce cement, no heat penetration during the combination period of making concrete is required.
(Submitted by Linda)

Overall, cement production involves some complex processes while limestone and clay are the main ingredients to produce cement. Moreover, concrete is produced using water, cement and sand in a concrete mixer.
Starting with the cement production, the first step is putting limestone and clay through the crusher in order to crush them to make powder content. Then, this powder content pass via a cylinder-shaped container for mixing and then passed to another cylinder equipment to be rotated in heat near a heat source, the resulting product is passed via a grinder to make cement and finally, it is packed in bags.
Turning to concrete production, by mixing multiple items in a large barrel-shaped container which include 15% cement, 10% water, 25% sand and 50% gravels which is consist of small stones in order to produce concrete as the final product.
These two processes are similar in using materials from earth crust with help from machines, however, the process in the first diagram, the cement is an output product, whereas, it is an input material in the second flow diagram of making concrete that water participates as a key element.
In the process of manufacturing cement, limestone and clay are crushed initially before relinquishing their product – powder that mixer and heater machines are ready to blend and rotate to finally drop into the grinder. Subsequently, the cement product is ready to be packed for sales. On the other hand, the concrete is a paste that requires all four key materials with an appropriate proportion which definitely constitutes Gravel of 50 percent, Sand of 25 percent, cement of 15 percent and essential water of 10 percent. This mixture results in concrete after rotating for a short period of time.
Overall, cement producing mechanism involves four complex processes and a number of tools are used for that whereas concrete production requires only a mixer.
In the first stage of cement production, the powder of limestone and clay, two essential raw materials in cement making, is mixed in a mixer after being crushed in a crusher. This powder is further passed through a rotating heater where constant heat is applied. The heated mixture is then smashed in a grinder after being bagged.
According to the second diagram, the cement is used in concrete production where a fixed quantity of water, cement, sand and gravel (small stones) are mixed together. 15% of cement is used along with 10% of water, 25% of sand and 50% of gravel. These raw materials are then poured into a mixture where it constantly rotates and makes strong concrete for the construction of any structure of a building.
The provided diagrams depict the manufacturing process of cement and how it could be used to make concrete for construction purpose.
Overall, there are six steps in the cement-making process and concrete production is comparatively easier as it involves combining the right proportion of different ingredients.
According to the first diagram, limestones and clays are two essential raw materials for the cement-making process. They are put on a crushing machine and turned into powder. Meanwhile, the powder is relinquished through a mixer and then put to a rotating heater where heat is supplied externally. Then that powder is sent into a grinder machine which produces the materials we call cement.
On the final stage, the cement is packed and ready for commercial use. Production of concrete is done in a machine called a concrete mixer. The process mixes 15% cement, 10% water, 25% grains of sand and 50% gravel (small stones). All those raw materials are poured into the concrete mixer which continuously rotates to form concrete.
Report